Mathématiques

Géométrie

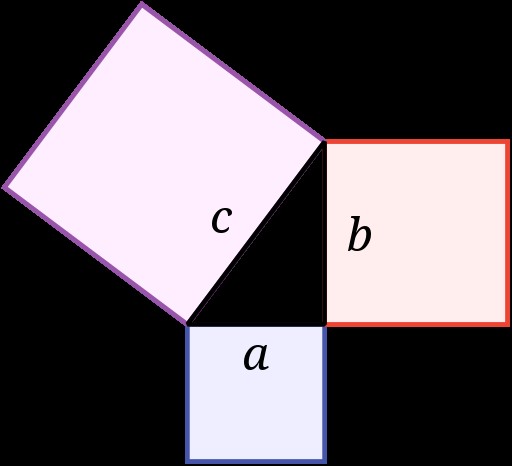
La géométrie étudie les figures, et plus particulièrement ce qui concerne leurs propriétés rigides. En tant que science déductive, elle commence, tout comme les mathématiques elles-mêmes, avec les Grecs. Les lignes droites, les triangles, les cercles, les sphères et les cubes sont parmi les premières figures étudiées. Un théorème typique, c’est-à-dire une affirmation générale obtenue par déduction, est qu’un triangle rectangle est caractérisé par la propriété de Pythagore (par exemple le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés).

Au début de la période de 600 avant notre ère jusqu’à 100 ans après notre ère, la théorie des sections coniques (ellipses, hyperboles, paraboles) se développe, tout comme la trigonométrie, qui est importante en astronomie. De plus, des formules pour calculer l’aire et le volume de figures particulières sont découvertes et prouvées. Les principaux développements ultérieurs sont l’introduction de la géométrie analytique (Descartes) et de la théorie de la courbure (Gauss), qui est la notion centrale de la géométrie différentielle. Par comparaison, la découverte de la géométrie non euclidienne est mineure.

En géométrie analytique, les points d’un plan sont désignés par deux coordonnées, soit les distances aux deux axes, et les figures familières deviennent le lieu géométrique des points qui résolvent une équation algébrique. La géométrie s’intègre ainsi à l’algèbre et la voie est ouverte à l’introduction d’espaces de dimensions arbitrairement larges, importants en mécanique. Dans sa forme la plus simple, la courbure est un nombre attaché à une surface en un point. Plus la surface est plate, plus ce nombre (positif pour une sphère, négatif pour une surface en dos d’âne) est petit.

Topologie

La topologie étudie les propriétés des figures ou des espaces qui sont invariantes sous l’effet de la déformation. Elle connait ses plus grands succès avec les dimensions supérieures, et elle étudie les espaces en y attachant des invariants algébriques et numériques. Par exemple, des surfaces orientées fermées sont caractérisées par leur genre (g). Pour la surface d’une balle, g = zéro; celui d’un beigne est g = un; et celui d’un pretzel est g = deux. La classification des espaces tridimensionnels, d’un intérêt beaucoup plus actuel, est encore incomplète. La formule de Gauss-Bonnet établit un rapport caractéristique entre la topologie et la géométrie : l’intégrale d’une courbe tracée sur une surface fermée est égale à quatre Pi (un-g).

Algèbre

L’algèbre étudie les propriétés générales des solutions d’une ou de plusieurs équations; l’arithmétique, ou la théorie des nombres, est l’étude des solutions dans des domaines spécifiques de nombres : par exemple les solutions de xⁿ + yⁿ = zⁿ dans les nombres entiers, comme dans la conjecture de Fermat. L’algèbre linéaire, la théorie hautement développée des équations du premier degré, joue un rôle important dans l’ensemble des mathématiques. La notion de valeur propre et de vecteur propre, qui apparaissent géométriquement comme les axes principaux d’un ellipsoïde, est cruciale. Toute l’algèbre est imprégnée du concept de groupe, une collection d’éléments qui peuvent être multipliés, comme les opérations sur un cube de Rubik. La théorie des groupes finis progresse fortement ces dernières années.

Analyse

L’analyse commence par le calcul différentiel et intégral, le calcul des vitesses et des tangentes (dérivées), des longueurs, des surfaces et des distances parcourues (intégrales), et des maximums et des minimums. La notion centrale est celle d’une fonction qui exprime la façon dont une variable dépend d’une autre. On ne peut calculer explicitement l’intégrale d’un très petit nombre de fonctions. Les problèmes qui accompagnent les fonctions algébriques ont grandement influencé le développement de la géométrie et de l’arithmétique.

Une équation différentielle relie une fonction à ses dérivées. Des équations différentielles se posent dans toutes les branches de la science. L’équation est ordinaire s’il n’y a qu’une variable indépendante et deux des problèmes fondamentaux sont la stabilité et l’existence de solutions périodiques. Nos connaissances sur le sujet sont vastes, mais les données empiriques, trouvées par ordinateur, dépassent notre compréhension théorique.

L’équation différentielle est dite partielle s’il y a plusieurs variables indépendantes. Les équations différentielles aux dérivées partielles apparaissent dans l’étude de la propagation des ondes et de la matière. En dépit d’une énorme théorie, certains phénomènes fondamentaux, tels que la turbulence, échappent encore à notre compréhension; on leur applique souvent des idées venant de la théorie des probabilités, qui constitue une discipline en soi. Les dérivées et les intégrales exigent l’usage de limites, comme le développement des fonctions dans les séries infinies, telle qu’une série de puissances ou une série de Fourier. Celle-ci exprime une fonction sous la forme d’une somme infinie de sinus et de cosinus, et est indispensable dans l’étude d’équations différentielles aux dérivées partielles.